在当今数字化与智能化飞速发展的时代,各行各业都在积极探索利用先进技术提升服务质量与效率。对于像拜耳集团旗下的上门除虫服务品牌“虫虫拜拜(byepest)”这样的企业来说,如何优化服务流程、合理配置资源,以满足日益增长的市场需求,成为了摆在面前的重要课题。在这一背景下,深入研究并创新下单预测及路线排划技术,具有至关重要的意义。
“虫虫拜拜(byepest)”业务开展伊始,上门服务的调度主要依赖人工与客户沟通并分配给工程师,此方式暴露出诸多弊端:
1) 多方沟通的协同效率极度低下;
2) 工程师每日的接单量严重受限;
3) 上门时间不确定导致的客户投诉率居高不下。
随着需求的爆发式增长,这种传统的服务调度模式已难以适应现有的业务规模。
那么,如何借助技术手段实现从客户下单至工程师分配再到上门服务的全自动化流程,通过算法优化实现工程师资源的高效合理配置,达成降本增效的目标呢?
1. 技术关键:两大难题待解
预测算法旨在解决在给定特定某天已确定的上门服务集合以及当天工程师的日程安排信息的前提下,判断当天某个特定地点在哪些时间点具备下单条件的问题。
路线排划算法需解决在已知服务单分布和可用工程师的情况下,如何将所有服务单合理分配给工程师,以满足某一最优条件,例如使工程师的转移距离总和最短。
无论是下单预测还是路线排划,均需考虑以下约束条件:
1) 工程师的等级需不低于服务单靶标的等级要求;
2) 工程师的服务半径限制在离家不超过 m 千米的范围内,即工程师仅能承接特定半径范围内的服务单;
3) 服务单之间的转移距离不得超过 n 千米,以避免工程师在路途上耗费过多时间和精力。
如何在多种约束条件下准确判断特定地点在给定条件下的下单时间点,以及如何在已知条件下合理分配服务单以满足最优条件,是核心难点。
2. 现有借鉴:他山之石的思考
下单预测当前存在类似场景,例如:
客户上门场景:如博物馆参观预约,通常采用固定额度预约模式,即在特定时间点(段)设定特定数量的预约名额,每当有客户预约则名额相应减少,当名额用尽则无法再预约。
快递或外卖行业:一般采用下单即时绑定服务人员的模式,主要依据附近人员的实时位置信息进行即时分配。
然而,与上述场景不同的是,“虫虫拜拜(byepest)”服务单均需至少提前一天预约上门,且服务单密度不足以支撑如快递行业那样一人负责一个小区的业务模式,工程师基本需要在全城范围内活动,因此难以建立预约额度与工程师数量之间的直接关联。
比如,早上 8 点在某一地点下了一个服务时长为 1 小时的服务单,必然会占用一名符合等级的工程师,由于服务单之间存在距离限制,显然会对 9 点及之后一段时间内的下单产生影响。也就是说,可预约额度应随服务单的下达而呈现不规则的动态变化,在我们的技术方案中引入了一个全新的概念——“容量”。
而路径规划,是计算机研究课题中运动规划的重要研究内容之一。例如,旅行商问题(TSP)即为路径规划的典型案例,其描述了如何规划路线以使旅行商以最短行走距离遍历给定城市集合,且每个城市仅访问一次的问题。解决此类问题的主要算法包括传统算法、图形学方法、智能仿生学算法等。
任何单一的路径规划算法在实际应用中的路径规划问题上均存在较大局限性。针对“虫虫拜拜(byepest)”路线排划的特殊限制,需采用混合算法予以解决。
3. 下单预测的创新解法:“容量”思路
预测算法本质上是判断某个地点l在时间t是否具备下单条件的问题。
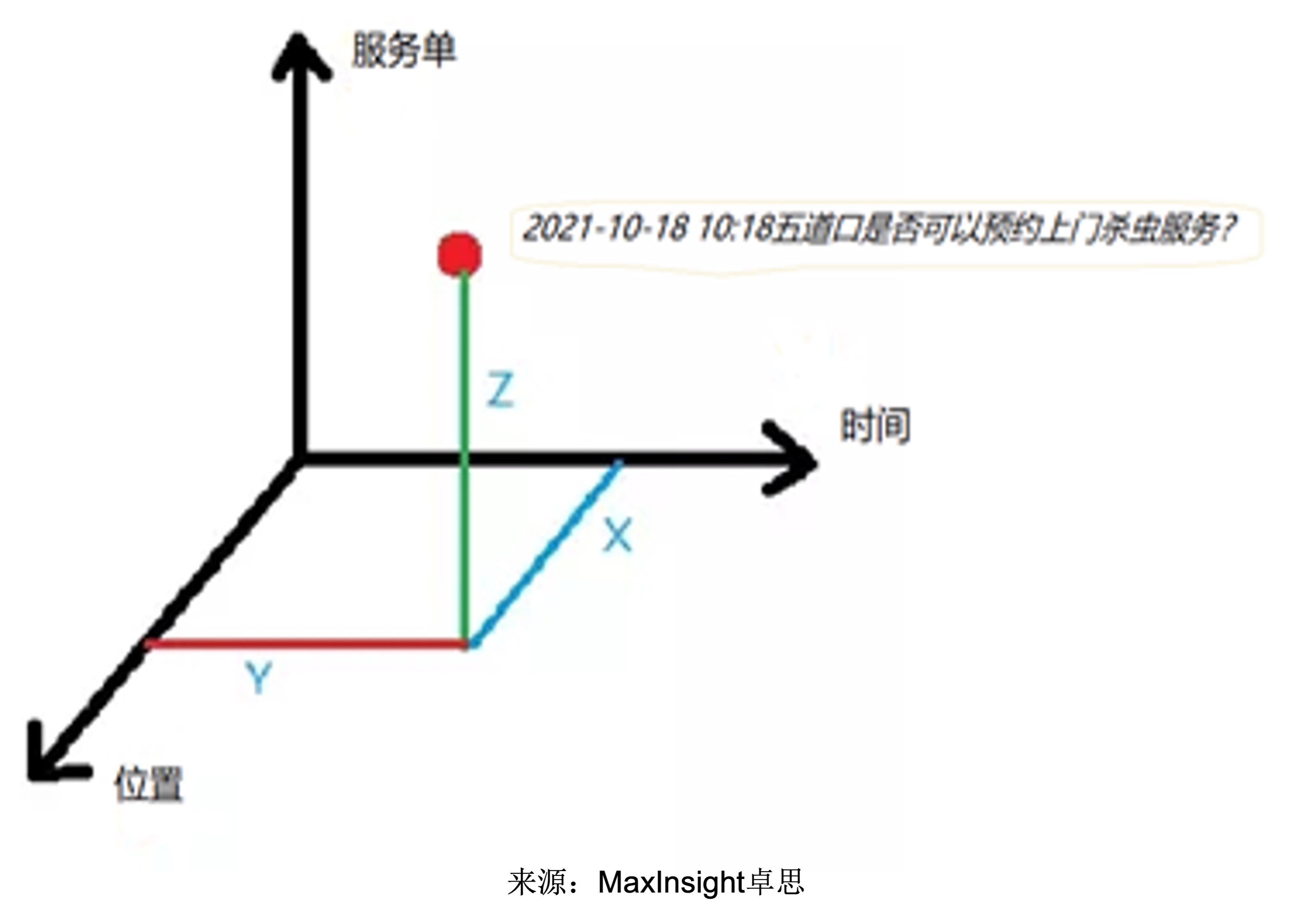
地点l在某个时间点t是否可下单实际上取决于满足条件的工程师人数K是否大于1。预测的精准性至关重要,倘若简单地为K设置一个固定上限值,若设置过小则无法充分发挥工程师的工作效能,设置过大则会导致下达过多订单而无法妥善安排的问题。不难理解,K的值由已下达订单的等级、时间、位置等信息共同决定,应是一个随订单下达而动态变化的量,因此我们的问题转化为如何动态精准计算K的值。
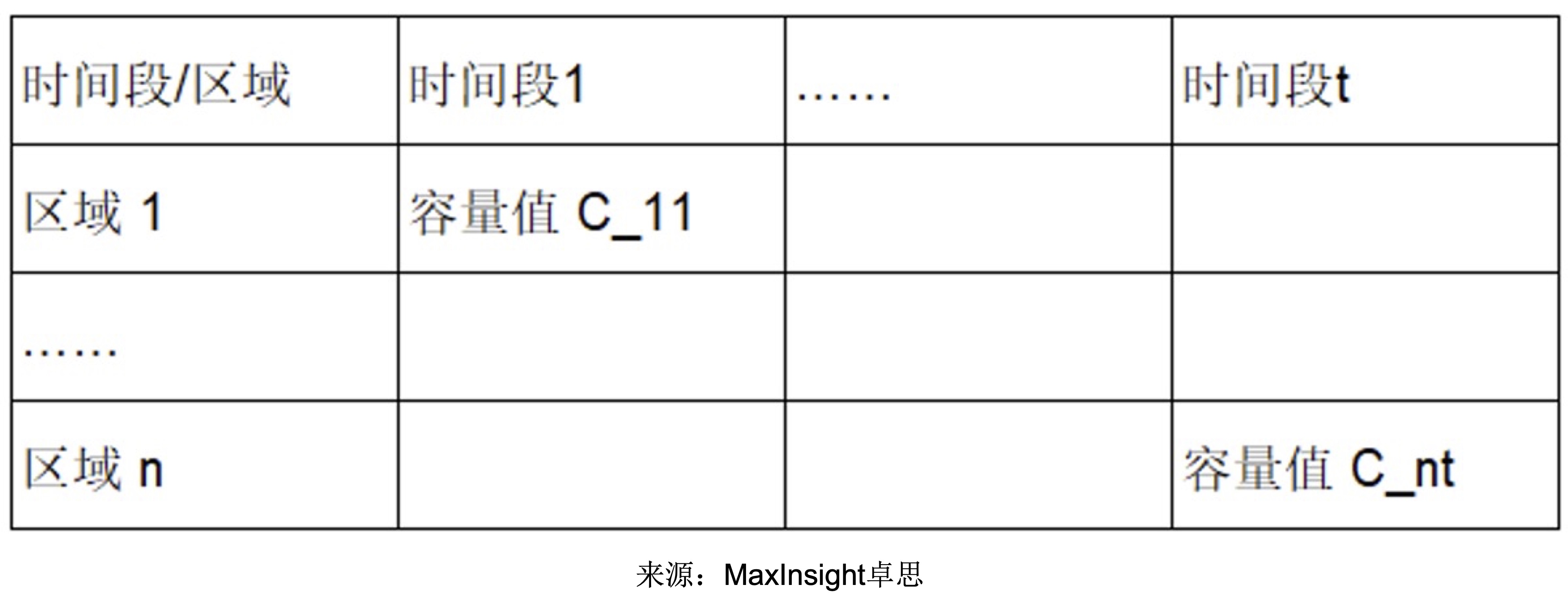
为解决上述问题,我们引入了一个全新概念——容量,用 C 表示,用于预估在某个时间点(段)某个区域可安排的工程师数量。若事先将城市划分为不同的小区域,那么整个城市的容量可以表示为矩阵:
预估的过程使用了“漏斗模型”,如下图所示:
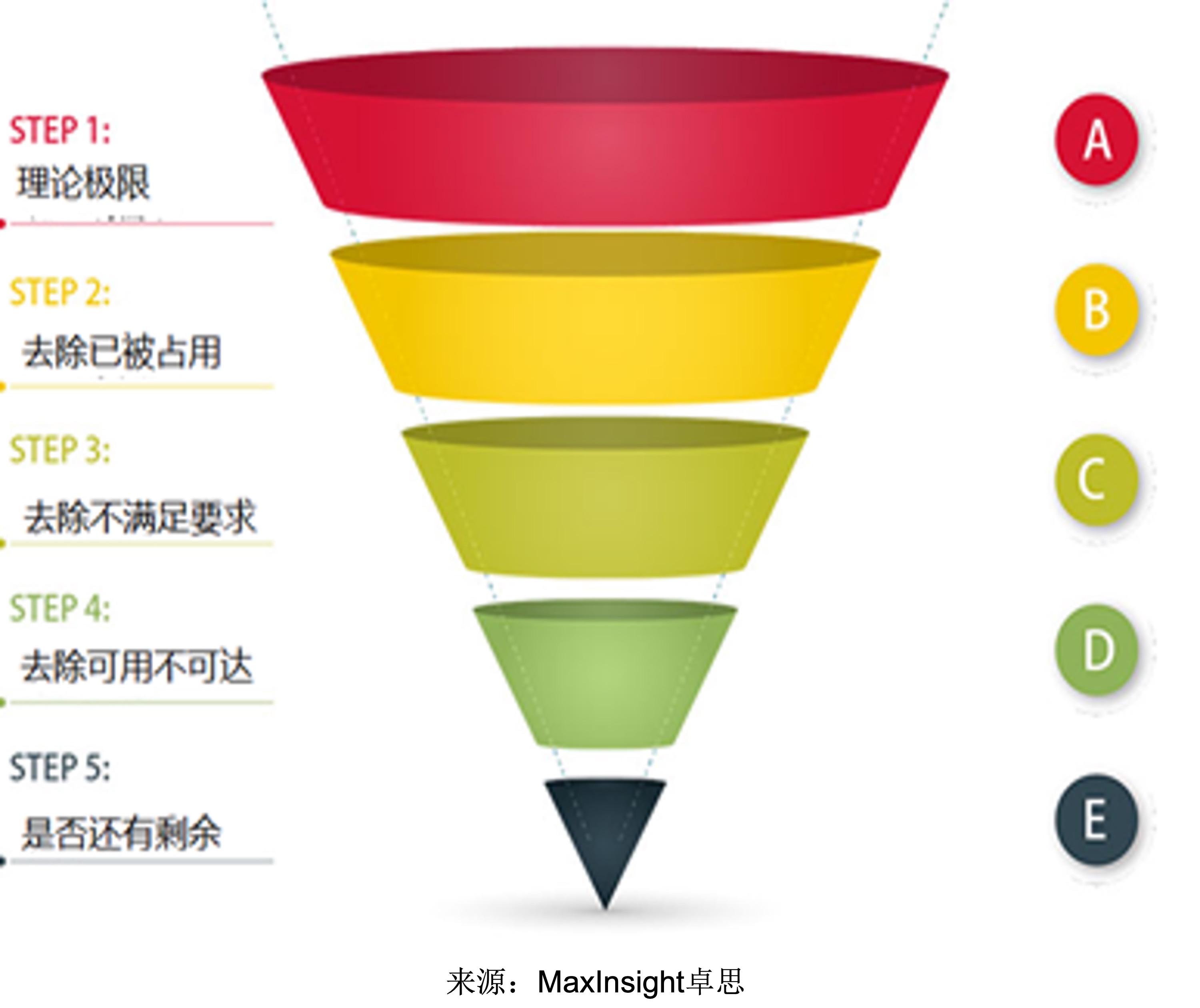
以某个地点某个时间点所在区域的容量计算为例:
1) 确定该地点可服务的工程师集合A,即驻地距离小于服务半径的工程师集合。
2) 获取该时间点内能够服务的工程师集合B,即该时间点空闲的工程师集合(依据排班信息)。
3) 取两者的交集 D=A∩B。
4) 结合时间上临近且已下达的可能影响当前预测的服务单,计算与当前预测服务单的衔接关系,从D中剔除前往不可达已下达服务单所需的工程师。
5) 得到C=len(D)-当前小区块该时间点已下达的订单数。
若最终计算得出的容量C>=1,则认为该时间地点允许下单。
为确保预测的实时性与高效性,采用缓存机制对容量信息进行离线计算并缓存,用户选定地点后可在毫秒级时间内迅速查询出各个时间点的容量。
更新时机为服务单或工程师考勤信息发生更改时,更新方法为对影响容量矩阵中的元素进行部分更新,同时操作可能引发的冲突是需要注意的潜在问题。
4. 路线排划的优化算法选择及更优解
路线排划算法旨在解决在给定服务单分布和可用工程师的情况下,如何将服务单分配给工程师以使某一最优条件得到满足(如工程师的转移距离最短),本质上是一个在多重限制条件下的不同起点的多旅行商问题(MTSP)。
在解决上述提到的优化问题时,传统优化算法和智能优化算法均在考虑范畴。
基于梯度的传统优化算法具有计算效率高、可靠性强、成熟度高等优点,是一类应用广泛且极为重要的优化算法。但是,传统优化算法在处理复杂、困难的优化问题时存在较大局限性。
智能优化算法通常是基于生物智能或物理现象构建的随机搜索算法,此类算法对目标函数和约束的连续性与凸性要求较低,甚至有时对是否具有解析表达式都不要求,对计算中数据的不确定性具有较强的适应能力。
鉴于要解决的问题较为复杂,此处优先选用智能算法中的遗传算法。遗传算法的原理在此不再赘述,接下来着重阐述如何运用遗传算法解决我们的路线排划问题:
1) 初始化:随机生成一批初始“染色体”,每个染色体代表一种可能的工程师路线分配方案。
2) 适应度函数:定义一个适应度函数用于评估每个染色体的质量。在本问题中,适应度函数可以设定为所有工程师行驶总距离的倒数(因我们期望最小化总距离)。此外,需要确保不违反任何约束条件(例如,工程师等级高于服务单的要求等级),若某个染色体违反约束,则将其适应度设定为极低值。
3) 选择:依据适应度函数,选取一部分染色体进行繁殖。存在多种选择策略,如轮盘赌选择、锦标赛选择等。
4) 交叉(杂交):通过特定方式对两个染色体进行交叉操作,生成新的染色体。例如,随机选定某个点,然后交换两个染色体在该点之后的所有元素。
5) 突变:以较小的概率随机改变某个染色体的部分内容。例如,随机交换两个服务单的分配。
6) 迭代:重复上述选择、交叉和突变步骤,直至满足特定的停止条件(如达到预定的迭代次数,或者适应度函数已不再显著改善)。
尽管遗传算法是解决组合优化问题的有力工具,但其收敛速度较慢,且无法确保找到全局最优解,通常只能获取相当不错的近似解。面对复杂的限制条件,寻找全局最优解的难度进一步加大,我们还需结合问题特点探寻更优解法。
我们路线排划的最大特点是服务单的开始时间固定,且在时间上具有衔接性,开始时间靠前的服务单必然能够找到开始时间靠后的后续服务单,如下图所示:
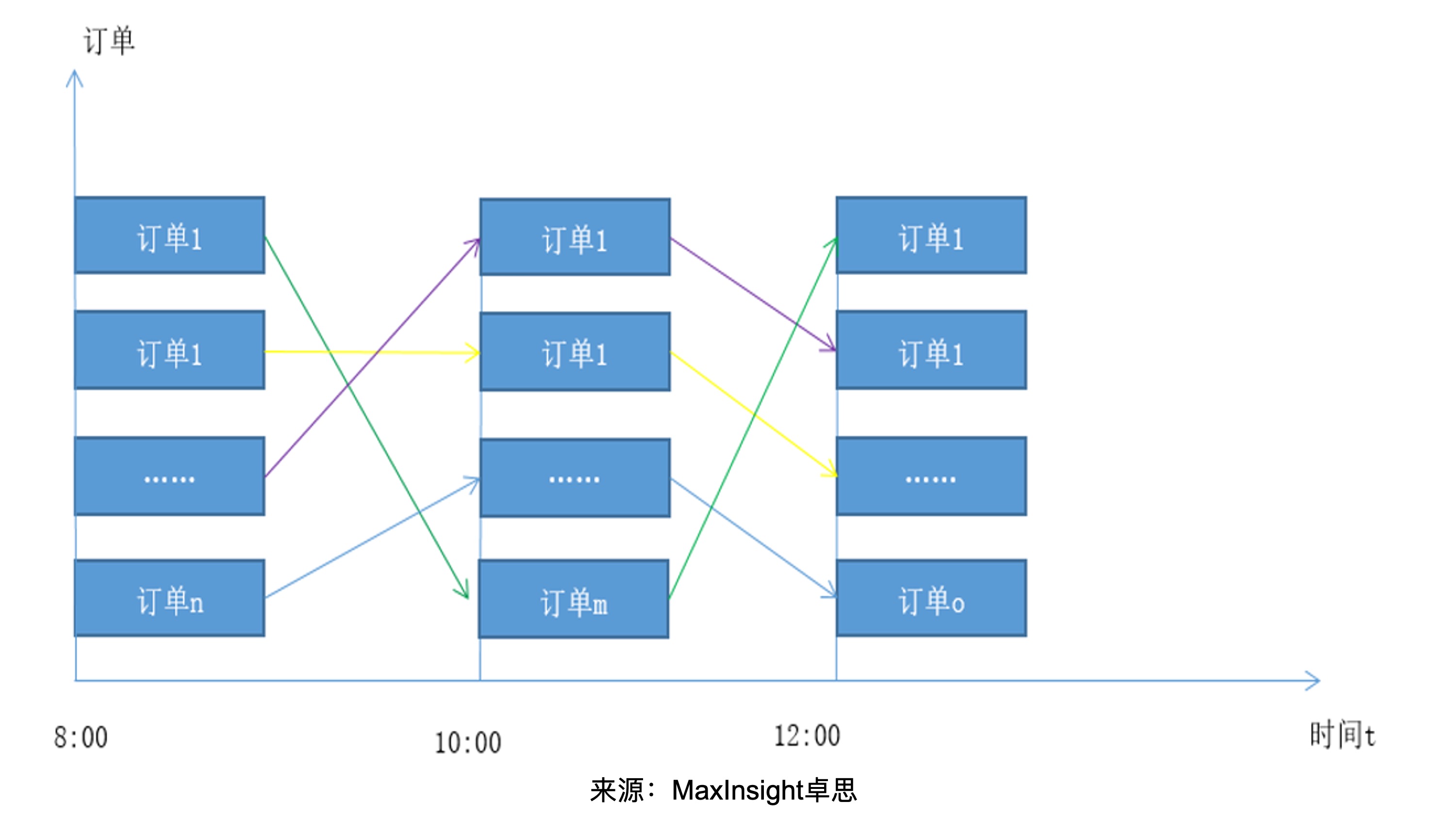
在路线排划的过程中,我们以时间线上的服务为一批次,然后插入已确定的路线中,此过程可抽象为m*n(m个任务分配给n个人)的任务分配过程,解决这一过程我们运用了匈牙利算法,即给定m个路线slot(萝卜坑),如何将某一时间线的n个订单(萝卜)插入其中以使总cost最小。
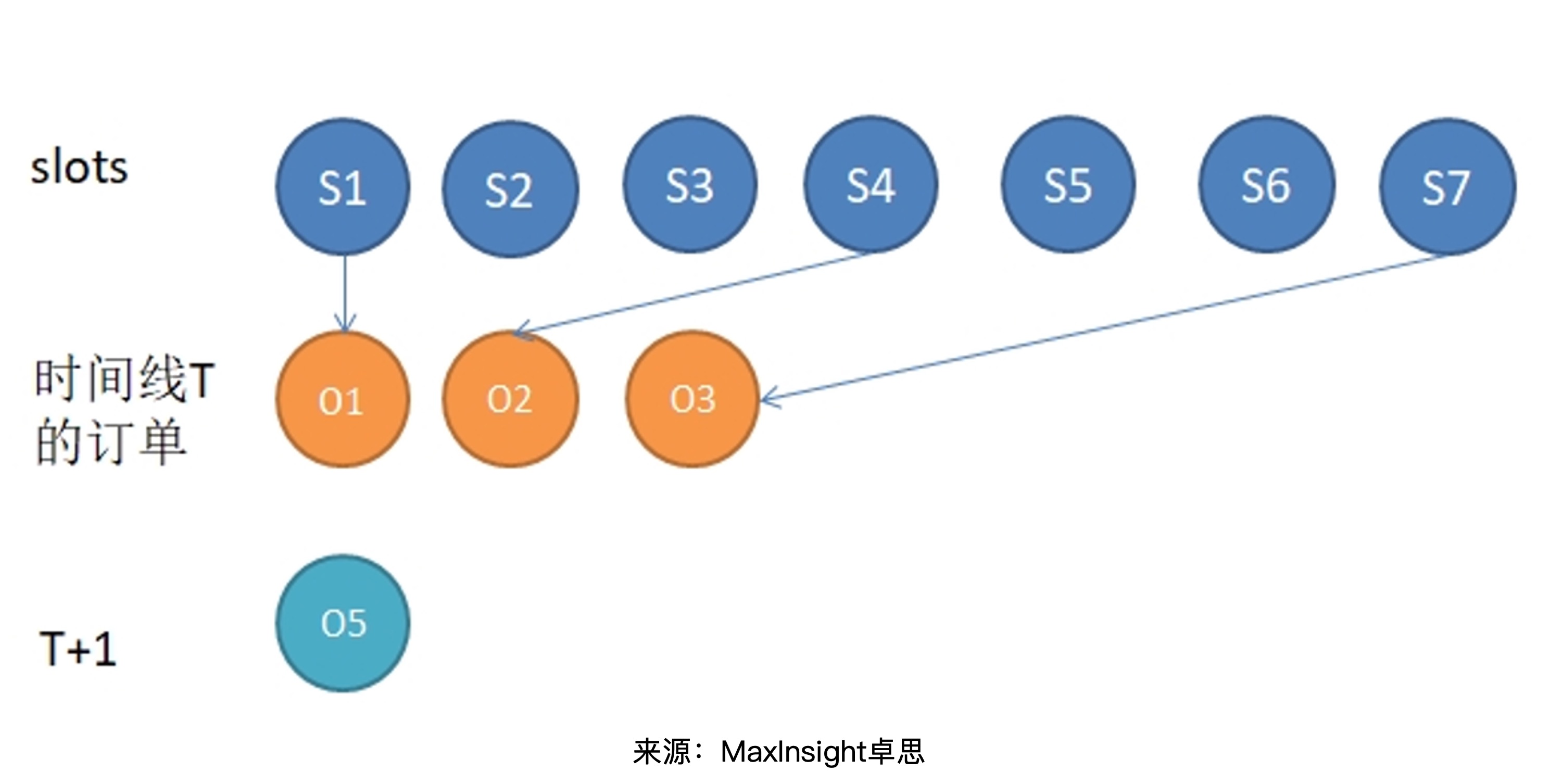
扩展至整个寻求最优路线的过程,可以视作是一个依照时间线推进的网格搜索过程,最终的路线即为时间线上同一颜色串联的服务序列。
综上所述,通过对“虫虫拜拜(byepest)”下单预测及路线优化技术的深入剖析和创新探索,我们在提高服务效率、优化资源配置方面取得了阶段性成果。这一成功实践不仅为“虫虫拜拜(byepest)”自身的持续发展奠定了坚实基础,对于其他企业和行业也具有重要的借鉴意义。企业在面临类似的资源调度和优化问题时,可以参考我们引入的新概念新算法新思路,根据自身业务特点进行灵活调整和创新。
未来,我们将继续深化技术研究,积极与各方交流分享经验,希望能为推动整个行业的技术进步和服务质量提升贡献力量,共同创造更加高效、智能的服务模式。